
สรุปคณิตศาสตร์ที่ต้องเจอในฟิสิกส์
ถ้าจะเริ่มเรียนรู้ฟิสิกส์ คณิตศาสตร์เปรียบเสมือนเครื่องมือหนึ่งที่จะช่วงน้องๆในการคำนวณทำให้มองเห็นภาพในการแก้โจทย์ปัญหาได้ง่ายมากยิ่งขึ้น โดยบทความนี้พี่จะรวบรวม คณิตศาสตร์สำหรับฟิสิกส์แยกเป็นข้อๆให้น้องๆได้เตรียมตัวเพิ่มความพร้อม
สารบัญ :
รูปแบบต่างๆของตัวเลข
รูปแบบต่างๆ ของตัวเลข
ตัวเลข อาจเขียนได้หลายแบบ แต่แบบที่จำเป็นต้องรู้จัก มี3แบบ คือ เศษส่วน ทศนิยม เปอร์เซนต์
การแปรผันตรงและการแปรผกผัน
การแปรผันตรงและแปรผันผกผันเป็นความสัมพันธ์ระหว่างปริมาณสองปริมาณ เมื่อปริมาณหนึ่งเปลี่ยนแปลง อีกปริมาณหนึ่งก็จะเปลี่ยนแปลงตามไปด้วย
ใช้ในการเปรียบเทียบความสัมพันธ์และใช้เพื่อหาแนวโน้ม
การแปรผันตรง
ปริมาณทั้งสองปริมาณจะเปลี่ยนแปลงไปในทิศทางเดียวกัน คือเพิ่มขึ้นหรือลดลงพร้อมกัน
ตัวอย่างเช่น ระยะทางที่เดินทางเพิ่มขึ้นเมื่อเวลาที่ใช้เดินทางเพิ่มขึ้น
สูตรความสัมพันธ์แบบแปรผันตรงตัวอย่าง y = kx
การแปรผันผกผัน
ปริมาณทั้งสองปริมาณจะเปลี่ยนแปลงไปในทิศทางตรงข้ามกัน คือเพิ่มขึ้นเมื่ออีกปริมาณหนึ่งลดลง และลดลงเมื่ออีกปริมาณหนึ่งเพิ่มขึ้น
ตัวอย่างเช่น ความดันของแก๊สลดลงเมื่อปริมาตรของแก๊สเพิ่มขึ้น
สูตรความสัมพันธ์แบบแปรผันผกผันตัวอย่าง y = k/x
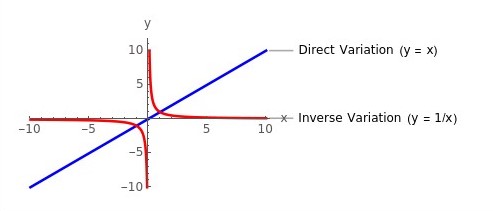
การแปรผันตรงรูปแบบอื่นๆ
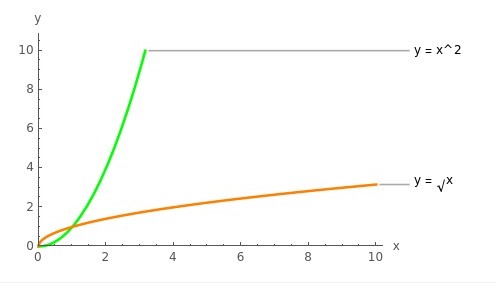
การแปรผันผกผันรูปแบบอื่นๆ
การแก้สมการ
การแก้สมการทั่วไปคือการหาค่าของตัวแปร
x ที่แทนค่าลงในสมการแล้วทำให้สมการมีค่าเท่ากับ 0 การย้ายข้างคือการย้ายตัวแปรหรือค่าคงที่จากด้านซ้ายของสมการไปด้านขวาของสมการ โดยรักษาความสัมพันธ์ของตัวแปรนั้นไว้
หลักการย้ายข้าง
เมื่อย้ายข้างใหเเปลี่ยนเครื่องหมายหน้าตัวที่ย้าย (มาจากเราดำเนินการทั้ง2ข้างให้เท่ากัน)
เครื่องข้างหน้าเป็น บวก ย้ายข้าง ให้เปลี่ยนเป็น ลบ
เครื่องข้างหน้าเป็น ลบ ย้ายข้าง ให้เปลี่ยนเป็น บวก
เครื่องข้างหน้าเป็น คูณ ย้ายข้าง ให้เปลี่ยนเป็น หาร
เครื่องข้างหน้าเป็น หาร ย้ายข้าง ให้เปลี่ยนเป็น คูณ
การแก้สมการหลายตัวแปร
ใจความสำคัญคือดูตัวแปรที่โจทย์ให้มา โจทย์ต้องการอะไร แล้วหาคำตอบของสมการแรกจากตัวแปรที่มีแล้วนำไปแทนในอีกสมการ
เลขยกกำลังและลอการิทึม
เลขยกกำลัง (Exponents)
เลขยกกำลัง \( a^n \) หมายถึงการคูณฐาน \( a \) ด้วยตัวมันเอง \( n \) ครั้ง. นี่คือคุณสมบัติหลักของเลขยกกำลัง:
ผลคูณของเลขยกกำลัง (Product of Powers):
$$ a^n \cdot a^m = a^{n+m} $$
อัตราส่วนของเลขยกกำลัง (Quotient of Powers):
$$ \frac{a^n}{a^m} = a^{n-m} $$
เลขยกกำลังของเลขยกกำลัง (Power of a Power):
$$ (a^n)^m = a^{n \cdot m} $$
เลขยกกำลังของผลคูณ (Power of a Product):
$$ (ab)^n = a^n \cdot b^n $$
เลขยกกำลังของอัตราส่วน (Power of a Quotient):
$$ \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n} $$
ลอการิทึม (Logarithms)
ลอการิทึม \( \log_a(x) \) คือการหาค่าของ \( n \) ที่ทำให้ \( a^n = x \). นี่คือคุณสมบัติหลักของลอการิทึม:
การเปลี่ยนฐาน (Change of Base Formula):
$$ \log_a(x) = \frac{\log_b(x)}{\log_b(a)} $$
ที่นี่ \( b \) คือฐานใด ๆ ที่คุณเลือกใช้, โดยทั่วไปจะใช้ฐาน 10 หรือ e (ฐานของลอการิทึมธรรมชาติ).
ลอการิทึมของผลคูณ (Product Rule):
$$ \log_a(xy) = \log_a(x) + \log_a(y) $$
ลอการิทึมของอัตราส่วน (Quotient Rule):
$$ \log_a\left(\frac{x}{y}\right) = \log_a(x) – \log_a(y) $$
ลอการิทึมของเลขยกกำลัง (Power Rule):
$$ \log_a(x^n) = n \cdot \log_a(x) $$
ลอการิทึมของฐานเดียวกัน:
$$ \log_a(a) = 1 $$
$$ \log_a(1) = 0 $$
ตรีโกณมิติ
ตรีโกณมิติ
สูตรพื้นฐาน:
สูตรสำหรับการคำนวณ Sin(θ), Cos(θ) และ Tan(θ) คือ:
Sin(θ) = (ข้างตรง)ข้าม / (ตรงข้ามมุม)ฉาก
Cos(θ) = (ข้างประ)ชิด / (ตรงข้ามมุม)ฉาก
Tan(θ) = (ข้างตรง)ข้าม / (ข้างประ)ชิด
สูตร Pythagorean:
สมการสำหรับความสัมพันธ์ระหว่าง Sin(θ) และ Cos(θ) คือ:
Sin²(θ) + Cos²(θ) = 1
สูตรเพิ่มเติมสำหรับ Tan(θ) และ Sec(θ) คือ:
1 + Tan²(θ) = Sec²(θ)
การเปลี่ยนแปลงเรขาคณิตและตรีโกณมิติ:
สูตรสำหรับการเปลี่ยนแปลงค่า Sin, Cos และ Tan คือ:
Sin(90° – θ) = Cos(θ)
Cos(90° – θ) = Sin(θ)
Tan(90° – θ) = Cot(θ)
กฎของสามเหลี่ยม:
สูตรสำหรับกฎไซน์และกฎคอไซน์ คือ:
กฎไซน์ (Law of Sines): a/Sin(A) = b/Sin(B) = c/Sin(C)
กฎคอไซน์ (Law of Cosines): c² = a² + b² – 2abCos(C)
เรขาคณิต
เรขาคณิต
สูตรพื้นฐาน:
สูตรสำหรับการคำนวณพื้นที่และปริมาตรคือ:
พื้นที่สี่เหลี่ยมผืนผ้า: กว้าง × ยาว
พื้นที่สามเหลี่ยม: 0.5 × ฐาน × สูง
พื้นที่วงกลม: πr² (r คือรัศมี)
ปริมาตร:
สูตรสำหรับการคำนวณปริมาตรของรูปทรงต่างๆ คือ:
ปริมาตรลูกบาศก์: ข้าง³
ปริมาตรทรงกระบอก: πr²h (r คือรัศมี, h คือความสูง)
ปริมาตรทรงกลม: 4/3πr³
เรขาคณิตวิเคราะห์:
สูตรสำหรับการคำนวณในเรขาคณิตวิเคราะห์ คือ:
สมการของเส้นตรง: y = mx + c (m คือความชัน, c คือจุดตัดกับแกน y)
ระยะทางระหว่างจุดสองจุด: √[(x₂ – x₁)² + (y₂ – y₁)²]
จุดกึ่งกลางของเส้นตรง: [(x₁ + x₂)/2, (y₁ + y₂)/2]



