คณิต ที่ต้องเจอใน TPAT3

ในที่TPAT3 ในเรื่องของคณิตศาสตร์ เราจะต้องมีพื้นฐานทางคณิต ดังนี้
การแก้สมการอสมการ อัตราส่วนร้อยละ ตรรกศาสตร์ และการคิดเป็นเหตุเป็นผล ตรีโกณและเรขาคณิต อนุกรม

การแก้สมการ และ อสมการ

–การแก้สมการ ส่วนนี้ที่ต้องรู้จักเพราะเราจะได้รู้เรื่องของระบบจำนวน และ เพื่อที่น้องๆจะได้ วิเคราะห์โจทย์ และสร้างสมการตัวแปร และ แทนค่าได้อย่างถูกต้อง เช่น ถ้าเรามีสมการ x + 2 = 5, เราต้องหาว่า x มีค่าเท่าไหร่
-การแก้อสมการ รู้จักกราฟเส้นแสดงช่วงคำตอบของอสมการ เช่น x > 3
วิธีทำ

การใช้กราฟเส้นเพื่อแสดงช่วงคำตอบของอสมการเป็นวิธีที่ดีในการทำให้เข้าใจแนวคิดทางคณิตศาสตร์ได้ง่ายขึ้น นี่คือขั้นตอนพื้นฐานในการวาดกราฟเส้นเพื่อแสดงช่วงคำตอบ:

1. เลือกอสมการ: เริ่มต้นด้วยการเลือกอสมการที่คุณต้องการแสดงในกราฟ เช่น x > 3

2. วาดแกนหลัก: วาดแกนหลักบนกระดาษหรือใช้ซอฟต์แวร์วาดกราฟ เช่น แกน x ที่แสดงค่าตัวแปร

3. ทำเครื่องหมายจุดหรือช่วง: สำหรับอสมการ x > 3, คุณจะทำเครื่องหมายบนแกน x ที่จุด 3 ตัวอย่างเช่น สามารถใช้จุดวงกลมที่ไม่เต็ม (○) ที่จุด x = 3 เพื่อแสดงว่า 3 ไม่รวมอยู่ในช่วงคำตอบ

4. เน้นช่วงที่เป็นคำตอบ: ในกรณีนี้ คุณจะเน้นช่วงที่อยู่ด้านขวาของจุด 3 เพื่อแสดงว่าช่วงคำตอบคือค่า x ที่มากกว่า 3

5. แสดงด้วยเส้นหรือลูกศร: วาดเส้นหรือลูกศรตามช่วงที่เป็นคำตอบ ในตัวอย่างนี้ จะเป็นลูกศรที่ชี้ไปทางขวาจากจุด 3

6. ตรวจสอบความถูกต้อง: ตรวจสอบให้แน่ใจว่ากราฟของคุณแสดงช่วงคำตอบของอสมการอย่างถูกต้อง

การใช้กราฟเส้นในลักษณะนี้ช่วยให้ผู้เรียนเห็นภาพชัดเจนของช่วงคำตอบและเข้าใจวิธีการแก้อสมการได้ดีขึ้น.

ตัวอย่างโจทย์

อัตราส่วนร้อยละ

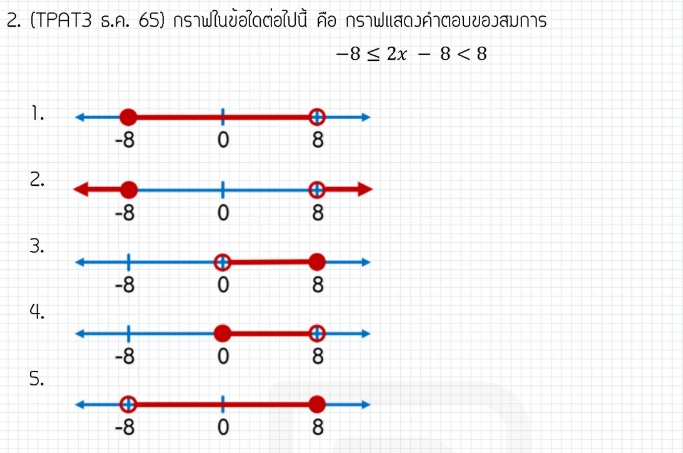
–อัตราส่วนร้อยละ ให้บ้างทีคำถามอาจไม่ได้ต้องการคำตอบตรงๆ เราจึงต้องแปลงอัตราส่วนร้อยละให้เป็น เป็นโจทย์ กำไล ขาดทุน ร้อยละ รายได้ รายจ่าย
ไม่ยากส่วนใหญ่มักเล่นคำในภาษาไทย

ตรรกศาสตร์ และ การคิดเป็นเหตุเป็นผล 

–ตรรกศาสตร์ และ การคิดเป็นเหตุเป็นผล  โดยใช้หลักความเป็นจริงในการพิจารณา หรือพิจารณาตามกฏ

น้องต้องจำตรางนี้ให้ได้

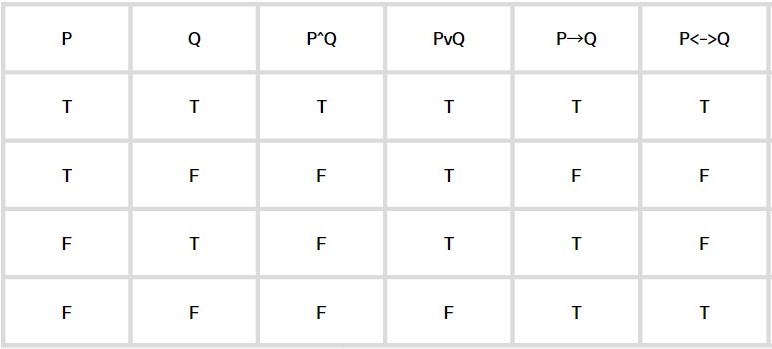
สรุป

P และ Q (AND)” จะเป็นจริง (True) เมื่อทั้ง P และ Q เป็นจริง

P หรือ Q (OR)” จะเป็นจริงเมื่อ P หรือ Q หรือทั้งคู่เป็นจริง

P ถ้าและเฉพาะถ้า Q (IFF)” จะเป็นจริงเมื่อ P และ Q มีค่าเท่ากัน

ไม่ P (NOT P)

ตัวอย่างโจทย์

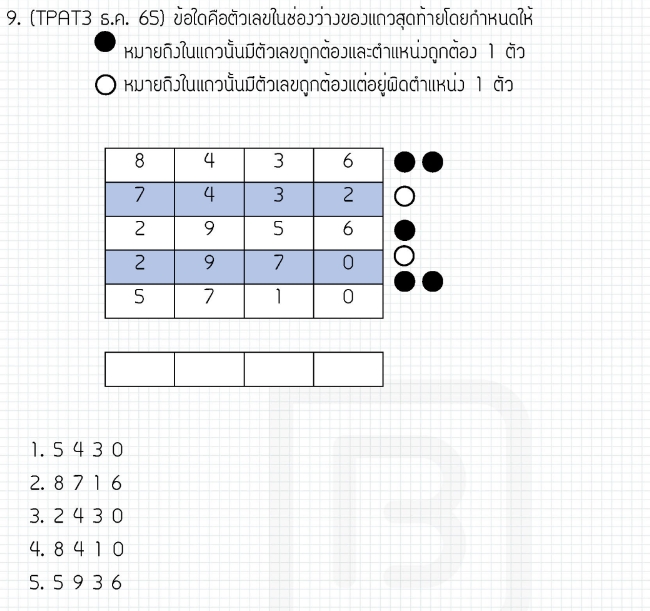
–ตรีโกณและเรขาคณิต: หัวข้อหลักๆจะมี เรื่องของการวัดและรูปทรง ใช้ในการหาขนาดของสิ่งต่างๆ เช่น มุม, พื้นที่, และปริมาตร ตัวอย่างเช่น ถ้าเรามีสามเหลี่ยม และรู้ความยาวฐานและความสูง เราสามารถหาพื้นที่ได้

ตรีโกณมิติ

ตรีโกณมิติ
สูตรพื้นฐาน:

สูตรสำหรับการคำนวณ Sin(θ), Cos(θ) และ Tan(θ) คือ:
Sin(θ) = (ข้างตรง)ข้าม / (ตรงข้ามมุม)ฉาก
Cos(θ) = (ข้างประ)ชิด / (ตรงข้ามมุม)ฉาก
Tan(θ) = (ข้างตรง)ข้าม / (ข้างประ)ชิด

สูตร Pythagorean:
สมการสำหรับความสัมพันธ์ระหว่าง Sin(θ) และ Cos(θ) คือ:
Sin²(θ) + Cos²(θ) = 1
สูตรเพิ่มเติมสำหรับ Tan(θ) และ Sec(θ) คือ:
1 + Tan²(θ) = Sec²(θ)

การเปลี่ยนแปลงเรขาคณิตและตรีโกณมิติ:
สูตรสำหรับการเปลี่ยนแปลงค่า Sin, Cos และ Tan คือ:
Sin(90° – θ) = Cos(θ)
Cos(90° – θ) = Sin(θ)
Tan(90° – θ) = Cot(θ)

กฎของสามเหลี่ยม:
สูตรสำหรับกฎไซน์และกฎคอไซน์ คือ:
กฎไซน์ (Law of Sines): a/Sin(A) = b/Sin(B) = c/Sin(C)
กฎคอไซน์ (Law of Cosines): c² = a² + b² – 2abCos(C)

ตัวอย่างโจทย์

เรขาคณิต

เรขาคณิต
สูตรพื้นฐาน:
สูตรสำหรับการคำนวณพื้นที่และปริมาตรคือ:
พื้นที่สี่เหลี่ยมผืนผ้า: กว้าง × ยาว
พื้นที่สามเหลี่ยม: 0.5 × ฐาน × สูง
พื้นที่วงกลม: πr² (r คือรัศมี)

ปริมาตร:
สูตรสำหรับการคำนวณปริมาตรของรูปทรงต่างๆ คือ:
ปริมาตรลูกบาศก์: ข้าง³
ปริมาตรทรงกระบอก: πr²h (r คือรัศมี, h คือความสูง)
ปริมาตรทรงกลม: 4/3πr³
เรขาคณิตวิเคราะห์:
สูตรสำหรับการคำนวณในเรขาคณิตวิเคราะห์ คือ:
สมการของเส้นตรง: y = mx + c (m คือความชัน, c คือจุดตัดกับแกน y)
ระยะทางระหว่างจุดสองจุด: √[(x₂ – x₁)² + (y₂ – y₁)²]
จุดกึ่งกลางของเส้นตรง: [(x₁ + x₂)/2, (y₁ + y₂)/2]

อนุกรม

อนุกรม
เหมือนการเพิ่มหรือคูณตัวเลขการทำจะดำเนินการในรูปแบบอื่นๆต่อเนื่องกันไปเรื่อยๆ เหมือนกับการก่อสร้างบันไดขึ้นไปเรื่อยๆ ทีละขั้น แต่ละขั้นของบันไดจะมีตัวเลขที่เราได้คำนวณมา

1. อนุกรมผลบวก: นี่คือการเพิ่มเลขเข้าไปเรื่อยๆ ตัวอย่างเช่น 1 + 2 + 3 + 4 + … ในอนุกรมผลบวก เราจะเพิ่มจำนวนตามลำดับที่กำหนด เช่น เพิ่มทีละ 1, 2, หรืออื่นๆ
2. อนุกรมผลคูณ: หมายถึงการคูณตัวเลขเข้าไปเรื่อยๆ ตัวอย่างเช่น 2, 4, 8, 16, … ที่แต่ละขั้นเพิ่มขึ้นเป็นสองเท่าของขั้นก่อนหน้า
3. อนุกรมทั้งคงที่และไม่คงที่:

– อนุกรมคงที่: ตัวอย่างเช่น 1 + 1 + 1 + 1 + … ที่เราเพิ่มเลขเดิมไปเรื่อยๆ

– อนุกรมไม่คงที่: ตัวอย่างเช่น 1 + 2 + 4 + 8 + … ที่เราเพิ่มเลขที่เปลี่ยนแปลงไปเรื่อยๆ

4. อนุกรมสะสม: นี่คือการรวมผลรวมของอนุกรมจนถึงจุดหนึ่ง เช่น 1 + 3 + 6 + 10 + … ที่แต่ละจำนวนเป็นผลรวมของทุกจำนวนก่อนหน้านั้น

5. อนุกรม 2 ชุด: เป็นการนำอนุกรมสองชุดมาเรียงต่อกัน เช่น (1, 2, 3) และ (4, 5, 6) รวมกันเป็น (1, 2, 3, 4, 5, 6)
6. รูปแบบผสม: นี่คือการผสมผสานระหว่างการเพิ่ม (เช่น บวก) และการคูณ ตัวอย่างเช่น 2, 4 + 1, 8 + 2, 16 + 3, … ที่เราคูณสองเท่าและเพิ่มเลขตามลำดับ

-ENTRANCE (TCAS) Physics Pack รวมเนื้อหาฟิสิกส์ ม.ปลาย
– พิชิต TPAT3 Pack เล่ม 1+2
– ทดลองพิชิต TPAT3 Pack เล่ม 1+2